| 1. A team building exercise is conducted in a company XYZ. P, Q and R are three female members of this exercise, such that: i. Each of the three participants belongs either to team I or to team II. ii. Members of team I always speak truth and those of team II always lie. iii. P tells the HR department of company XYZ “Either I belong or Q belongs to a different team from the other two members”. Which participant’s belongingness to a particular team are you definitely sure of? |
Difficult |
| A. P B. Q C. R D. Can’t be determined |
View Answer
Answer: Option B
Explanation:
Two possibilities arise:
1. P tells the truth
Since P is speaking the truth, either she belongs to team I and Q & R belong to team II
or
Q belongs to team II and P & R belong to team I
Therefore from 1,
P € team I; Q, R € team II
or
P, R € team I; Q € team II
2. P tells a lie
In this case P surely belongs to team II and either all three belong to the same team (which has to be team II as P is definitely in team II)
or
R belongs to team I and P & Q belong to team II (because the statement that Q belongs to different team from the other two is false, and Q shares membership with either P or R; R is not responsible as P is surely a member of team II, and Q, therefore, is in the same team as P)
Therefore, from 2,
P, Q, R € team II
or
R € team I; P, Q € team II
Looking at all possibilities (from 1 and 2), we observe that Q always belongs to team II. Thus, we are sure about Q belonging to team II.
| 2. There are 5 different boxes with different weights. A person weighs them in pairs and the readings thus obtained are (in kgs): 110, 112, 113, 114, 115, 116, 117, 118, 120, 121. What is the weight of the heaviest box? | Difficult |
| A. 61 kg B. 59 kg C. 62 kg D. Can’t be determined |
View Answer
Answer: Option C
Explanation:
Since there are 10 readings and weighing is carried out in pairs, it implies that each pair includes two boxes, and each box is weighed 4 times.
-> 4(a+b+c+d+e) = 110+112+113+114+115+116+117+118+120+121 = 1156
-> a+b+c+d+e = 1156/4 = 289 —– ❶
Now a+b = 110 [smallest reading has to be the sum of the two lightest boxes]
and d+e = 121 [highest reading has to be the sum of the two heaviest boxes]
Putting values of a+b and d+e in —– ❶, we get
110+c+121 = 289 -> c = 58 —–❷
Now, 112 has to be the sum of a and c (since a<b)
-> a+c = 112 -> a+58 = 112 -> a = 54 —– ❸
Also, a+b = 110 -> 54+b = 110 -> b = 56 —– ❹
Now out of the 10 readings, 4 are odd which means that one of the boxes weighs an odd number, and the other four weigh even numbers. Since a, b and c are even with 54, 56 and 58 as their respective values, one of d and e will be weighing an odd number. Also, we know that d+e = 121
-> d or e will be an odd number with value 59 or 61 [it has to be more than 58, and it can’t be 63 because in that case one out of d or e will be 121-63 = 58, which is the value of c]
Thus, the possible values of d and e are either 60 and 61, or 59 and 62. However 60 is not a possible value. We have 120 as one of the readings, and that is possible if we add 62 and 58.
Thus, d = 59 and e = 62
The weights are 54, 56, 58, 59, 62.
Heaviest is 62 kg.
| 3. Four couples – C1, C2, C3, C4 – are made to sit around a circular table at seats which are equally spaced, such that: i. Mrs. C1 was embarrassed by Mr. C2, who sat next to her on her left. ii. Mr. C2 was embarrassed by Mrs. C3 who sat diametrically across him. iii. Mrs. C3 was embarrassed by the organizer (a woman), who was the only person to sit next to each one of a married couple. iv. The organizer was embarrassed by the only person to sit next to two men. Who embarrassed the organizer? |
Difficult |
| A. Mr. C3 B. Mrs. C2 C. Mr. C2 D. Can’t be determined |
View Answer
Answer: Option A
Explanation:
From i and ii, the following can be concluded:
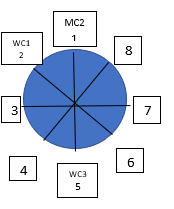
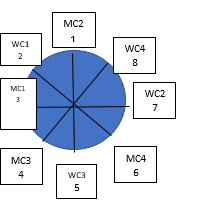
In the above arrangement 3, 4 and 6 would be occupied by MC1, MC3 and MC4 (in any order), leading to WC1 and WC3 each sitting next to two men, which is not possible.
Similarly, we try checking the feasibility of different arrangements with the organizer sitting at 3, 4, 6, 7 and 8, and conclude that the only feasible arrangement is as follows:
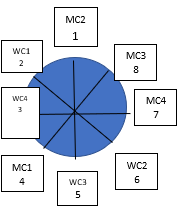
The above arrangement is the only arrangement satisfying all conditions. From this, we conclude that WC4 is the organizer (sitting in between WC1 and MC1 – one each of a married couple). MC3 is the only person sitting next to two men, and is therefore the person who embarrasses the organizer WC4. So, Mr. C3 is the answer.
Note: Seats 1 to 8 are only indicative of a cyclic sequence and are not fixed.
