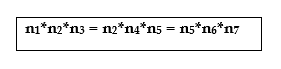| 1. Four people – Charu, her father, her husband, and their daughter – played a game of table-tennis (mixed doubles). At a particular moment in the game, one of them makes two statements: i. “I am directly across the net from the server’s daughter” ii. “My partner (on the same side of the net as I) is directly across the net from the receiver’s father” Who makes these statements? |
Difficult |
| A. Charu B. Charu’s Father C. Charu’s Mother D. Charu’s Daughter |
View Answer
Answer: Option B
Explanation:
From i and ii, the server’s daughter has to be the receiver, and the daughter of both the server and the receiver’s father.
->Server’s daughter/receiver is Charu’s daughter
->Server is Charu
->The person directly across Charu is Charu’s husband
->The person directly across Charu’s daughter is Charu’s father.
The arrangement can be represented as under:
| Charu (Server) | Charu’s Father |
| Charu’s Husband | Charu’s Daughter (Receiver) |
Thus, the statements are made by Charu’s father
| 2. Company XYZ conducts a placement interview for 6 candidates A, B, C, D, E and F. i. A, B, c are males; D, E, F are females. ii. A and D are friends; B and E are friends; C and F are friends. iii. For each set of friends, the male friends is interviewed before his female counterpart. In how many ways can the interviews be conducted?A. 90 B. 36 C. 60 D. 72 |
Difficult |
View Answer
Answer: 90
Explanation:
Let M indicate a man and W indicate a woman. Following are the possible arrangements:
I.
MMMWWW
1 2 3 4 5 6
Three men can be interviewed in the first 3 slots in 3*2*1 = 6 ways; three women can be interviewed in the next three slots in 3*2*1 = 6 ways.
->Total number of ways in which the candidates can be interviewed = 6*6 = 36
II.
MWMWMW
1 2 3 4 5 6
Interviews at slots 1 & 2 can be conducted in 3 ways (M1W1, M2W2, M3,W3), at slots 3 & 4 in 2 ways (two out of the remaining), and at slots 5 & 6 in 1 way.
->Total number of ways in which the candidates can be interviewed = 3*2*1 = 6
III.
MMWMWW
1 2 3 4 5 6
Interview at slot 1 can be conducted in 3 ways (M1, M2, M3), at slot 2 in 2 ways (two of the remaining men), at slot 3 in 2 ways (corresponding to the two men in slots 1 & 2), at slot 4 in 1 way (the person remaining out of M1, M2, M3), at slot 5 in 2 ways (corresponding to any two of the remaining women), and at slot 6 in 1 way (the women who hasn’t been interviewed till now)
->Total number of ways in which the candidates can be interviewed = 3*2*2*1*2*1 = 24
IV.
MWMMWW
1 2 3 4 5 6
Interview at slot 1 can be conducted in 3 ways (any one of the three men), at slot 2 in 1 way (corresponding to the man who is interviewed at slot 1), at slot 3 in 2 ways (two of the remaining men), at slot 4 in 1 way (the man who yet remains), at slot 5 in 2 ways (any of the two remaining women), and at slot 6 in 1 way (the remaining woman)
->Total number of ways in which the candidates can be interviewed = 3*1*2*1*2*1 = 12
V.
MMWWMW
1 2 3 4 5 6
Interview at slot 1 can be conducted in 3 ways (any one of the three men), at slot 2 in 2 ways (two of the remaining men), at slot 3 in 2 ways (corresponding to the two men in slots 1 & 2), at slot 4 in 1 way (corresponding to the man whose counterpart is not interviewed at slot 3), at slot 5 in 1 way (the man who yet remains), and at slot 6 in 1 way (corresponding to the man who is interviewed
at slot 5)
->Total number of ways in which the candidates can be interviewed = 3*2*2*1*1*1 = 12
->Total number of ways in which the candidates can be interviewed = I+II+III+IV+V = 36+6+24+12+12 = 90
Note:
- While calculating the number of ways in which the interviews can be conducted for each of the 5 possibilities, we have applied the fundamental principle of counting, which states “If you have an event ‘a’ and another event ‘b’, then the total number of different outcomes for the events is a*b”.
- Finally, we add the number of ways corresponding to each of the 5 possibilities, because all these events are mutually exclusive i.e., one event excludes the possibility of occurrence of others.
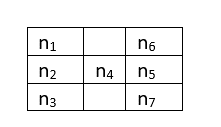
| 3. A magical grid comprises 7 digits n1, n2…..n7, all of which are distinct with any value from 0 to 9, as shown below:
The following equation holds true for the grid:
What values can n2 take? |
Difficult |
| A. 4 or 9 B. 3 or 9 C. 2 or 9 D. Can’t be determined |
View Answer
Answer: Option A
Explanation:
The first step here is to eliminate values which are not possible in the grid.
- 0 is eliminated because it will make one of the three triplets zero (n1 n2n3; n2n4n5; n5n6n7), and the other two triplets can’t be zero because we have only one zero in the set of possible values.
- 5 and 7 are eliminated because their occurrence in any of the triplets will make that triplet a multiple of 5 or 7 respectively and the remaining 2 triplets can’t be such multiples because there are no more 5s or 7s available (both 5 and 7 are prime and don’t have factors other than 1)
The remaining digits are: 1, 2, 3, 4, 6, 8, 9 which can be resolved into prime factors in the following ways:
1 -> 1
2 -> 2
3 -> 3
4 -> 2*2
6 -> 2*3
8 -> 2*2*2
9 -> 3*3
Thus, there are seven 2s, four 3s and one 1 in the grid. Out of the three triplets, n1n2n3 and n5n6n7 should have equal number of 2s and 3s if the product is the same, which is possible if each of the triplets has three 2s and two 3s as shown below:
n1*n2*n3 = 2*2*2*3*3
n5*n6*n7 = 2*2*2*3*3
Looking at the available digits we get the following values:
n1*n2*n3 = 4*2*9 —– ❶
n5*n6*n7 = 8*9*1 —– ❷
Now n4 will have a unique value of 2 because out of seven 2s and four 3s, all are taken but for one 2, which corresponds to the value of n4. Also, since the triplets have the same value, n2*n5 should be equal to 36, as n2*n4*n5 should be equal to 72. From ❶ & ❷, 36 is possible only as 4*9 or 9*4. Thus,
n2*n4*n5 = 4*2*9 OR 9*2*4
Hence, n2 can have two values i.e. 4 and 9.
Answer = 4, 9
Note:
With the above conditions, eight arrangements are possible as shown-

Possible values for n1 = 3, 6, 1, 8
Possible values for n2 = 4, 9
Possible values for n3 = 6, 3, 1, 8
Possible values for n4 = 2
Possible values for n5 = 9, 4
Possible values for n6 = 8, 1, 3, 6
Possible values for n7 = 1, 8, 6, 3