| 1. What is the sum of the first 50 terms of an A. P., whose first term is 3 and the common difference is 5? | Easy |
| A. 6275 B. 12550 C. 6200 D. None of these |
View Answer
Answer: Option A
Explanation:
∵ S50 = 1/2 ×50[2(3)+(50-1)5]=6275
| 2. If the nth term of a series is (n+3)/4, then the sum of the first 89 terms of this series is: | Easy |
| A. 1068 B. 2136 C. 1958 D. None of these |
View Answer
Answer: Option A
Explanation:
Here T1 = 1, T2 = 5/4, T3 = 6/4 …..
-> The series is in arithmetic progression with a =1, and d = 1/4
-> S89 =1/2 ×89[2(1)+(89-1)(1/4)]=1068
| 3. The sum of 4th and 16th elements of an A.P. is equal to the sum of the 7th, 12th and 14th elements of the same progression. Then which element of the series should necessarily be equal to zero? | Medium |
| A. 12th B. 13th C. 10th D. Can’t be determined |
View Answer
Answer: Option B
Explanation:
Let the A.P. be a, a+d, a+2d, ……
Now, Tn = a+(n-1)d
-> T4+T16 = T7+T12+T14
-> a+3d+a+15d = a+6d+a+11d+a+13d
-> a+12d = 0
-> T13 = 0
| 4. If the sum of the first 9 terms of an A.P. equals that of the first 11 terms, then what is the sum of the first 20 terms? | Easy |
| A. 32 B. 20 C. 0 D. None of these |
View Answer
Answer: Option C
Explanation:
From the given information,
(9/2)(2a+8d) = (11/2)(2a+10d)
-> 18a +72d = 22a+110d
-> 4a+38d = 0
-> 2a+19d = 0
Now, ∑20 = (20/2)(2a+19d) = 10*0 = 0
| 5. The sums of n terms of two arithmetic series are in the ratio (5n-3): (3n+15). What is the ratio of the sixth terms of the two series? | Medium |
| A. 1:1 B. 12:11 C. 13:12 D. None of these |
View Answer
Answer: Option C
Explanation:
Let the first series have a1 as the first term and d1 as the common difference, and the second series have a2 as the first term and d2 as the common difference.
Then, sum of n terms of the two series will be (n/2)( (2a1+(n-1)d1) and (n/2)(2a2+(n-1)d2) respectively.
From the given information,
(2a1+(n-1)d1)/(2a2+(n-1)d2) = (5n-3)/(3n+15) —–❶
Now, ratio of 6th terms will be (a1+5d1)/(a2+5d2).
(a1+5d1)/(a2+5d2) = 2a1+10d1/2a2+10d2 (Multiplying both numerator and denominator
by 2) —–❷
From ❶, if n = 11, then (2a1+10d1)/(2a2+10d2) = 13/12 —–❸
From ❷ & ❸, (a1+5d1)/(a2+5d2) = 13/12
| 6. Find the fourth term of the series 2, 5/2, 10/3,…… | Medium |
| A. 17/4 B. 26/5 C. 5 D. None of these |
View Answer
Answer: Option C
Explanation:
The reciprocals of the terms of the given series are 1/2, 2/5, 3/10,….
Or 5/10, 4/10, 3/10, ….., which are in A.P. whose common difference = (4/10)-(5/10) = -1/10
∴ Fourth term of this A.P.
= a+(n-1)d = (5/10) + (4-1)(-1/10) = 2/10 = 1/5
∴ Fourth term of the given series = 1/(1/5) = 5
| 7. What is the 49th term of the series 2+7+14+23+34+……? | Easy |
| A. 2000 B. 2999 C. 2498 D. None of these |
View Answer
Answer: Option C
Explanation:
Given series is [(22-2) +(32-2) +(42-2) +….]
-> Tn = (n+1)2-2
-> T99 = (49+1)2 – 2 = (50)2-2 = 2498
| 8. Find the sum of the first 10 terms of the series 1.32+2.52+3.72+……. | Difficult |
| A. 13695 B. 27390 C. 82170 D. None of these |
View Answer
Answer: Option A
Explanation:
The series formed by the first factors of the terms of the given series is 1, 2, 3, ……., whose nth term is n.
The series formed by the second factors of the terms of the given series is 32, 52, 72, …., whose nth term = [3 + (n-1)2]2 = (2n + 1)2
-> nth term of the given series = n(2n+1)2
Sum up to n terms = ∑[n(2n+1)2]=∑[n(4n2+4n+1)]
=4∑n3+4 ∑n2+∑n
= 4(n(n+1)/2]2 + 4[n (n+1) (2n+1)/6] + ½ n(n+1)
= [n(n+1)/6 ] [6n(n+1) + 4(2n+1) + 3]
=(1/6) n(n+1)(6n2+14n+7)
Putting n = 10, we get required sum = (1/6) (10)(11) (600+140+7)
= 13695
| 9. What is the value of the following expression? (1/22-1) + (1/42-1) + (1/62-1) + ………. (1/402-1) |
Difficult |
| A. 19/41 B. 20/41 C. 21/41 D. None of these |
View Answer
Answer: Option B
Explanation:
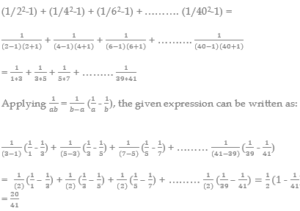
| 10. Consider the sequence of numbers a1, a2, a3……. to infinity where a1 = 61.22, a2 = -11 and ak= ak-1 – ak-2 for k≥3. What is the sum of the first 5402 terms of this sequence? | Difficult |
| A. 61.22 B. 11 C. 50.22 D. None of these |
View Answer
Answer: Option C
Explanation:
ak= ak-1 – ak-2 for k≥3
Thus,
a3 = a2 – a1
a4 = a3 – a2 = a2 – a1 – a2 = -a1
a5 = a4 – a3 = -a1 – (a2 – a1) = -a2
a6 = a5 – a4 = -a2 – (-a1) = a1 – a2
a7 = a6 – a5 = a1 – a2 + a2 = a1
Sum of first 6 terms = a1+a2+(a2-a1)-a1-a2+a1-a2 = 0
-> Sum of first 5400 terms = 0 (because the sum of every 6 terms is 0, and 5400 is a
multiple of 6). Thus 540th term will be a1 and 5402th term will be a2.
-> Sum of first 5402 terms = a1+a2 = 61.22 – 11 = 50.22
