| 1. Let U = {3, 7, 8, 17, 19, 27}. P1 represents the number of circular permutations of all the numbers in set U, where the adjacent numbers are relatively prime. P2 represents the number of linear permutations of all the numbers in set U, where the adjacent numbers are relatively prime. Determine the value of P2 – P1. |
Medium |
| A. 408 B. 204 C. 600 D. None of these |
View Answer
Answer: Option A
Explanation:
Only 3 and 27 are not relatively prime. The six numbers can be arranged linearly in 6! ways = 720
If 3 and 27 are adjacent then the number of permutations = 5!*2 = 120*2 = 240 ways
-> P2 = 720-240 = 480
Number of circular permutations of 6 numbers = 5! = 120
If 3 and 27 are adjacent to each other, the number of circular permutations = 2*4! = 48
-> P1 = 120-48 = 72
->P2-P1 = 480-72 = 408
| 2. There are 12 points marked on one straight line and 13 on another straight line parallel to the first line. Calculate the number of triangles that can be formed using vertices selected from these points.? | Easy |
| A. 2691 B. 897 C. 1794 D. None of these |
View Answer
Answer: Option C
Explanation:
Required number of ways = (12C2*13) + (13C2*12) = 1794
Note
We add here because the events are mutually exclusive.
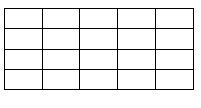
| 3. What is the number of rectangles in the following grid?
|
Medium |
| A. 150 B. 120 C. 80 D. None of these |
View Answer
Answer: Option A
Explanation:
A rectangle with m rows will have (m+1) horizontal lines; similarly, n columns will generate (n+1) vertical lines. A rectangle of any size in this grid is created from 2 horizontal lines and 2 vertical lines.
-> Number of rectangles will correspond to the number of ways in which 2 horizontal lines can be chosen from (m+1) horizontal lines and 2 vertical lines can be chosen from (n+1) vertical lines.
-> Number of rectangles = R = m+1C2 * n+1C2 = ((m+1)*m*(m-1)!)/((m+1-2)*2!) * ((n+1)*n*(n-1)!)/((n+1-2)*2!) = (m(m+1)*n(n+1))/4
The given grid is a rectangle of size 4*5 [4 rows, 5 columns]
Now, the number of rectangles, R, in a rectangular grid of size m*n is given by:
R = (m*(m+1)*n*(n+1))/4
Here, m = 4 and n = 5
R = (4*5*5*6)/4 = 150
| Directions for questions 4 and 5: Read the following data and answer the questions accordingly:
An engineering college has the following break-up:
|
|||||||||||||||||
| 4. If all Mechanical students sit together, all Civil sit together and so do all Electrical, then what is the total number of ways in which they can be seated? | Easy |
| A. 27!*35!*38! B. 3!+(27!*35!*38!) C. 3!*27!*35!*38! D. None of these |
View Answer
Answer: Option C
Explanation:
Mechanical can sit in (5+20+10)! = 35! ways
Civil can sit in (3+15+20)! = 38! ways
Electrical can sit in (20+5+2)! = 27! ways
These 3 groups can be themselves arranged in 3! ways
Desired number of ways = 3!*35!*38!*27!
| 5. If no Mechanical engineer is allowed to sit next to another Mechanical engineer, find the total number of ways in which the students can be seated. | Medium |
| A. 100! B. 100!-(35!*66!) C. 35!*66! D. None of these |
View Answer
Answer: Option B
Explanation:
Total seating ways = (27+35+38)! = 100!
If we consider all the Mechanical engineers as 1, then the total number of students = 27+38+1 = 66, who can be arranged in 66! ways.
Therefore, no. of ways in which the Mechanical engineers sit together will be 66!*35! (within one group, they can be arranged in 35! ways)
Therefore, number of ways in which they are not together
100! – (35!*66!)
| 6. Alexa has 7 friends. In how many ways can she invite one or more than one at dinner? | Medium |
| A. 128 B. 127 C. 126 D. None of these |
View Answer
Answer: Option B
Explanation:
If she invites only one friend out of 7, she can do it in 7C1 ways; if she invites 2 friends, she can do it in 7C2 ways and so on. If she invites all her friends, she can do it in 7C7 ways.
Therefore, the total number of ways of inviting friends =
7C1+7C2+7C3+7C4+7C5+7C6+7C7
= 7C1+7C2+7C3+7C3+7C2+7C1+7C0 [nCr = nCn-r]
= 7 + (7*6)/(2*1) + (7*6*5)/(3*2*1) +(7*6*5)/(3*2*1)+ (7*6)/(2*1) + 7 + 1
= 7+21+35+35+21+7+1 = 127
| 7. In an examination, a candidate has to pass in each of the five subjects. In how many ways can he fail? | Easy |
| A. 31 B. 32 C. 33 D. None of these |
View Answer
Answer: Option A
Explanation:
The candidate can fail by failing in 1 or 2 or 3 or 4 or 5 subjects.
Therefore, required number of ways in which he can fail =
5C1+5C2+5C3+5C4+5C5
= 5C1+5C2+5C2+5C1+5C5 [nCr = nCn-r]
= 5+ (5*4)/(2*1)+(5*4)/(2*1)+ 5+1 = 31
| 8. A man has 7 relatives, 4 Indians and 3 foreigners. His wife also has 7 relatives, 3 Indians and 4 foreigners. In how many ways can he invite 3 Indians and 3 foreigners so that 3 of them are the man’s relatives and 3 his wife’s? | Difficult |
| A. 485 B. 340 C. 198 D. None of these |
View Answer
Answer: Option A
Explanation:
The various possibilities are shown in the table below:
| Man’s Relatives | Woman’s Relatives | |||
| Indians | Foreigners | Indians | Foreigners | |
| I. | 3 | 0 | 0 | 3 |
| II. | 2 | 1 | 1 | 2 |
| III. | 1 | 2 | 2 | 1 |
| IV. | 0 | 3 | 3 | 0 |
Number of ways for I = 4C3 * 4C3 —– ❶
(3 Indians, man’s relatives, can be selected from 4 Indians, man’s relatives in 4C3 ways; 3 foreigners, woman’s relatives, can be selected from 4 foreigners, woman’s relatives in 4C3 ways. Applying fundamental principle of counting*, total number of ways = 4C3 * 4C3)
Similarly, number of ways for II = 4C2*3C1*3C1*4C2 —– ❷
Similarly, number of ways for III = 4C1*3C2*3C2*4C1 —– ❸
Similarly, number of ways for IV = 3C3*3C3 —– ❹
Now, nCr = n!/(n-r)!r!
❶ = 4C3 * 4C3 = 4!/(3!*!) * 4!/(3!*!) = 4*4 = 16
❷ = 4C2*3C1*3C1*4C2 = 4!/(2!*2!) * 3!/(3!*1!) * 3!/(2!*1!) * 4!/(2!*2!) = (4*3)/2*3*3*(4*3)/2 = 324
❸ = 4C1*3C2*3C2*4C1 = 4!/(3!*1!) * 3!/(3!*1!) * 3!/(2!*1!) * 4!/(3!*1!) = 4*3*3*4 = 144
❹ = 3C3*3C3 = 1*1 = 1
Total = 16+324+144+1 = 485
Note
We add here because, ❶, ❷, ❸ and ❹ are mutually exclusive events (i.e., if one happens, the others do not happen).
9. You are required to place six Xs in a 3*3 square grid as shown below: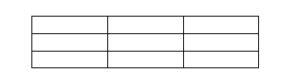 However, the constraint is that you need to fill each row and each column with at least one X, and there can be only one X in one square. In how many ways can this be done? |
Difficult |
| A. 84 B. 78 C. 54 D. None of these |
View Answer
Answer: Option B
Explanation:
6 Xs can be put in 9 boxes in 9C6 ways
Now 9C6 = 9!/(6!*3!) = (9*8*7*6!)/(6!*3*2) = 84
Also, there will be 6 ways in which one row or one column will be vacant.
Therefore, required number of ways = 84-6 = 78
| 10. From 6 men and 4 women a committee of 5 is to be formed. In how many ways can this be done if the committee is to include at least one woman, and if two particular women refuse to serve on the same committee. | Medium |
| A. 100 B. 160 C. 190 D. None of these |
View Answer
Answer: Option C
Explanation:
1W + 4M = 4C1*6C4 = 60 ways
2W + 3M = (4C2 – 1) *6C3 = 100 ways
3W + 2M = (4C3 – 2)*6C2 = 30 ways
Total = 60+100+30 = 190 ways