| 1. U is a universal set, while M and N are sets defined in the universal set, as per the following directions: U = {-8, 6, 1, -3, 9, 0, 4} M = {x/x > 0} N = {x/x < 4} What is the set M’ ∪ N’? |
Easy |
| A. {-8, -3, 6, 9, 4} B. {-8, -3, 0, 6, 9, 4} C. {-8, -3, 0, 6, 4} D. None of these |
View Answer
Answer: Option B
Explanation:
M = {6, 1, 9, 4}
-> M’ = {-8, -3, 0}
N = {-8, 1, -3, 0}
-> N’ = {6, 9, 4}
-> M’ ∪ N’ = {-8, -3, 0, 6, 9, 4}
| 2. If Pc is the set of all factors of c, and Qk is the set of all multiples of k, which of the following is/are true? I. P42 ∩ P54 = P6 II. Q6 ∩ Q9 = Q18 |
Difficult |
| A. I only B. II only C. Both I and II D. Neither I nor II |
View Answer
Answer: Option C
Explanation:
I. P42 ∩ P54 is the set comprising numbers that are common factors of 42 and 54 -> numbers that are factors of the HCF of 42 and 54 -> numbers that are factors of 6.
Hence, I is true.
II. Q6 ∩ Q9 is the set comprising numbers that are common multiples of 6 and 9 -> numbers that are multiples of the LCM of 6 and 9 -> numbers that are multiples of 18
Hence, II is true.
| 3. Out of a management class with 120 students, those who opted to study marketing also chose to study operations. However, none of the students selected both marketing and finance. 32 students decided to study operations and finance simultaneously. All the students in the class are enrolled in at least one of the three subjects. Additionally, the number of students studying exactly one subject exceeds that of students studying more than one subject. Determine the maximum and minimum number of students who could have exclusively chosen finance. | Difficult |
| A. 80, 0 B. 90, 0 C. 88, 0 D. 88, 1 |
View Answer
Answer: Option C
Explanation:
The following Venn Diagram can represent the information:
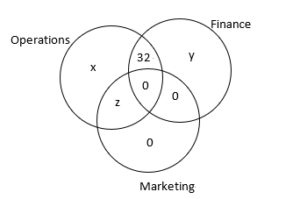
All students study at least one of the three subjects -> x+y+z+32 = 120 -> x+y+z = 88 —– ❶
The number of students who study exactly one of the three subjects is more than the number who study more than one of the three -> x+y > z+32 —– ❷
In the given options, the minimum value of y is 0.
Let us check for the feasibility of this value. If y=0, then from ❶, x+z=88, and from ❷, x>z+32. Both of these are possible. For example, x=87, y=0, z=1 is a permissible value set amongst many others.
With minimum y as 0, the maximum y value in the options is 90. However, from ❶, 90 is not a possible value. In fact, y can not have a value more than 88. So, we check for the feasibility of 88 as a value of y. If y=88, then from ❶, x=z=0, which is a possibility. Thus, the maximum value of y is 88.
| Direction for questions 4 and 5: Refer to the data below and answer the following questions.
A park that requires an entry fee of Rs 10 was frequented by 8000 students. Inside the park are three types of rides – P, Q, and R – each priced at Rs 10 per student. Out of the visitors, 1800 students enjoyed all three rides, while 3000 students experienced at least two of the rides. Remarkably, none of the students rode the same attraction more than once. From these student visits, the park generated total revenue of Rs 172000. |
|
| 4. How many students took no rides at all? | Medium |
| A. 1800 B. 7200 C. 3600 D. None of these |
View Answer
Answer: Option C
Explanation:
The amount collected from all those who took 2 or 3 rides =
(1800*30)+ ((3000-1800)* 20) = 78000
Entrance fee = 8000*10 = 80000
So, 172000 – (78000+80000) = 14000 must have been collected from 1400 people who took 1 ride @ Rs 10 per ride
-> 1400 students took one ride.
So, number of people who took no rides = 8000 – (1800+1200+1400) = 3600
| 5. If rides P, Q, and R are priced at Rs 10, 20, and 30, respectively, and all other information remains the same as in Q4, how many students took no rides? | Easy |
| A. 1200 B. 3600 C. 2400 D. Can’t be determined |
View Answer
Answer: Option D
Explanation:
The answer cannot be determined as it is dependent on the number of people who took rides P, Q, and R, respectively, and this is unknown.
| 6. If U = {8,10,9,2,3,-1,0,7} X = {8,10,3,-1} and Y = {-1,11,2,3}, find X’∩ Y’. | Easy |
| A. {-1,7} B. {0,3} C. {0,7} D. None of these |
View Answer
Answer: Option C
Explanation:
X’ = {11,2,0,7}
Y’ = {8,10,0,7}
-> X’∩ Y’ = {0,7}
| 7. How many numbers in the set {-6,0,3,5} satisfy the conditions |x-7|≤ 9 and |x+7|≤ 8, given that x is an integer? | Medium |
| A. 0 B. 1 C. 2 D. None of these |
View Answer
Answer: Option B
Explanation:
|x-7|≤ 9
-> -9 ≤x -7 ≤ 9
-> -2 ≤ x ≤ 16
Out of these values of x, the ones which satisfy the given set =P = {0,3,5}
Also, |x+7|≤ 8
-> -8 ≤ x+7 ≤8
-> -15 ≤ x ≤ 1
Out of these values of x, the ones which satisfy the given set = Q= {-6,0}
Required numbers = P ∩Q = {0}
Hence, only one number satisfies the given conditions.
Direction for questions 8 and 9: Refer to the data below and answer the following questions.
A group of children went on a trip where they could enjoy three types of rides – P, Q, and R. Among the children, 56 chose ride P, 46 went for ride Q, and 30 opted for ride R. Out of these children, 22 decided to experience both rides P and Q, 18 chose both rides P and R, and 16 children decided to take both rides Q and R. Notably, none of the children selected ride R exclusively.
| 8. How many children went on the trip? | Easy |
| A. 80 B. 68 C. 40 D. None of these |
View Answer
Answer: Option A
Explanation:
Let the number of children who took all three rides = x
Then, the information can be represented in the following Venn diagram:
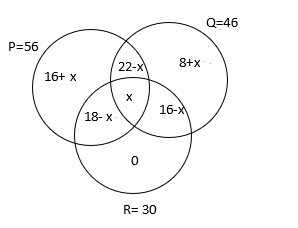
From the above diagram and the information in the question, we get 18-x+x+16-x = 30 -> x = 4
Thus, the Venn diagram can be reconstructed as under:
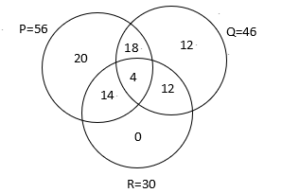
Number of children who went on the trip = 20+18+4+14+12+12+0 = 80
| 9. If each ride costs Rs.100, what is the total bill for the trip? | Medium |
| A. 13200 B. 4400 C. 8800 D. None of these |
View Answer
Answer: Option A
Explanation:
From the diagram in Q8,
Number of children who took only 1 ride = 20+12+0=32; Fare = 32*100 =3200
Number of children who took only 2 rides = 18+14+12 = 44; Fare = 44*2*100 =8800
Number of children who took only 3 rides = 4; Fare = 4*3*100 =1200
Total Fare = 3200+8800+1200 = Rs. 13200
| 10. Among a group of 200 students, 96 students have opted for physics, 72 students for chemistry, and 108 for mathematics. Of these, 38 students have taken physics and mathematics, 32 have chosen physics and chemistry, and 20 have decided on both mathematics and chemistry. What is the ratio of students who have taken physics but not mathematics and chemistry to those who have taken mathematics but not physics and chemistry? | Medium |
| A. 5:8 B. 5:7 C. 5:6 D. None of these |
View Answer
Answer: Option A
Explanation:
200 = n(P) + n(C) + n(M) – n(P∩C) – n(C∩M) – n(M∩P) + n(C∩M∩P)
200 = 96+72+108-32-20-38+ n(C∩M∩P)
200 = 276-90+ n(C∩M∩P)
-> n(C∩M∩P) = 14
n(P only) = n(P) – n(P∩M) – n(P∩C)+ n(P∩M∩C) = 96-38-32+14 = 40
n(M only) = n(M) – n(P∩M) – n(M∩C) + n(P∩M∩C) = 108-38-20+14 = 64
Required ratio = 40 :64 = 5:8
