| 1. A, B, C and D play three games such that: i. A and B are males; C and D are females. ii. The first game is played either between A and C, or between B and D, and these pairs are not possible in subsequent games. iii. A and C belong to city P; B and D belong to city Q. iv. The males win two games and the females win one game. v. Winners continue to play and losers are knocked out of playing subsequent games. vi. City P players win more games as compared to city Q players. vii. Each player plays at least one game. Which player does not lose even a single game? |
Difficult |
| A. B B. D C. A D. C |
View Answer
Answer: Option B
Explanation:
Case I: First game played between A and C
If C wins this game, then the seven winning outcomes, for the three games will be:
1. C B D
2. C D B
3. C B B
4. C D D
5. C C B
6. C C D
7. C C C
All these seven outcomes are not possible as they contradict one or more conditions under which the games are played. For example, outcomes 1, 2, 4, 5, 6, 7 contradict condition iv.; outcome 3 contradicts condition vi.
If A wins the game, then the various winning outcomes for the games will be:
1. A B D
2. A D B
3. A B B
4. A D D
5. A A B
6. A A D
7. A A A
Out of these seven outcomes 1 & 2 violate condition vi; 3, 4, 5, 7 violate condition iv, but 6 is possible because it satisfies all conditions. For 6 to be true A beats C in the first game; then A beats B in the second game and D beats A in the third game. Thus, D is the person who does not lose any game.
Case II: First game played between B and D
If B wins the game, then the various winning outcomes are:
1. B C A
2. B A C
3. B C C
4. B A A
5. B B C
6. B B A
7. B B B
Here, 3, 4, 6, 7 violate condition iv; 1, 2 & 5 violate condition ii. So, B can’t win the first game. If D wins the first game, then the various winning outcomes are:
1. D C A
2. D A C
3. D C C
4. D A A
5. D D C
6. D D A
7. D D D
Here, 1, 2, 3, 5, 6, 7 violate condition iv; 4 violates condition ii, because for this to be true D has to beat B in the 1st game; A has to beat D in the 2nd game and C has to beat B in the 3rd game. However, A and C can’t be paired again in 2nd or 3rd games, as per condition iv.
Looking at both the cases, and the various outcomes therein, we conclude that only outcome AAD in case I is possible, where D is undefeated.
| 2. Roger and Bain play a game of cards, where each person in his turn can pick 1, 2, 3 or 4 cards. The person who gets to pick the last card loses the game. If they are both logical and play to win, then how many cards should Roger pickup from a regular pack of 52 cards, if he makes the first move, so that he ensures a win? | Medium |
| A. 1 B. 2 C. 3 D. Can’t be determined |
View Answer
Answer: Option A
Explanation:
Bain loses the game if he gets to pick the last card, or if he gets to pick a card when there are 6 cards left, or when there are 11 cards left.
Thus, we conclude that Bain loses if he gets to pick a card when there are (5k+1) cards left to pick from.
So, in order to win, Roger has to pick as many cards as will leave (5k+1) cards for Bain to pick from.
-> Roger should pick 1 card so that (5*10) +1 = 51 cards are left for Bain to choose from. Thus, Roger should pick 1 card.
| 3. P, Q and R often go out for lunch together, such that: i. Each of them orders either drink A or drink B before lunch. ii. If P orders drink A, then Q orders the same drink that R orders. iii. If Q orders drink A, then P orders the drink that R does not order. iv. If R orders drink B, then P orders the drink that Q orders. Who orders the same drink every time before lunch and which one? |
Medium |
| A. Q, Drink A B. P, Drink B C. R, Drink A D. Can’t be determined |
View Answer
Answer: Option B
Explanation:
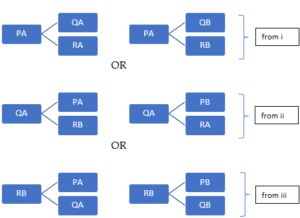
Where PA means that P orders drink A etc.
From above, there are 6 possibilities:
| PA | PA | QA | QA | RB | RB |
| QA | QB | PA | PB | PA | PB |
| RA | RB | RB | RA | QA | QB |
| ❶ | ❷ | ❸ | ❹ | ❺ | ❻ |
Applying ii, iii and iv to the above 6, we are left with only 2 possibilities – ❹ & ❻. Others can be eliminated; for example, condition iii will eliminate ❶, condition iv will eliminate ❷, condition ii will eliminate ❸ & ❺. So, we are left with only ❹ & ❻. In both P orders drink B.
