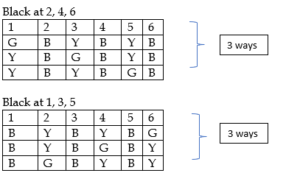
| 1. How many different arrangements are possible for a line of flags consisting of one green flag, three black flags, and two yellow flags, given the following conditions: i. No two adjacent flags are of the same colour. ii. The flags at both ends of the line are of different colours. |
Easy |
| A. 8 B. 12 C. 6 D. None of these |
| 2. In a game of chess, Alexa wants to place her two horses, such that one is on a white square, other on a black square, and the two horses must not lie in the same row or column. In how many ways can she do so? | Medium |
| A. 56 B. 768 C. 651 D. None of these |
| 3. What is the total number of solutions to a*b*c = 30, where a, b and c are positive integers? | Medium |
| A. 21 B. 27 C. 30 D. None of these |
| 4. What is the sum of all the possible numbers of 4 digits formed by using the digits 3, 5, 5, 6 using each digit once? | Difficult |
| A. 63327 B. 57000 C. 256 D. None of these |
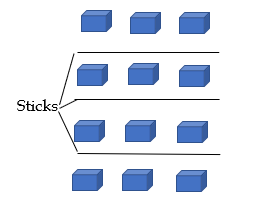
| 5. In an array organized by 12 students, there are 3 sticks—two black and one white. The students form rows of 3 each and hold the sticks in a way that the sticks are positioned between the rows, with 6 students holding each stick. Given that each student can take any position in the array, how many different arrangements are possible? | Medium |
| A. 12!*6 B. 12!*2 C. 12!*3 D. None of these |
| 6. In how many ways can 6 pencils be distributed among 5 students if a student may get any number of pencils? | Easy |
| A. 15625 B. 7776 C. 625 D. None of these |
| 7. In a specific entrance test pattern, there were 10 questions, each consisting of two parts: Part A and Part B. What is the total number of possible selections a student can make when answering one or more questions on the paper. Please note that the student must choose either Part A or Part B when attempting any question. | Medium |
| A. 59048 B. 19682 C. 999 D. None of these |
| 8. How many 5-digit numbers can be formed by using all the digits (only once) 0, 2, 4, 7 and 5, such that the numbers are not divisible by 75? | Medium |
| A. 96 B. 82 C. 14 D. None of these |
| 9. How many numbers less than 10000 can be constructed such that only the digits 5, 6, 7, 8, 9 are used in these numbers (repetitions allowed) and the numbers are divisible by four? | Difficult |
| A. 781 B. 650 C. 775 D. None of these |
| 10. Let x be the number of different 4-digit numbers divisible by 3, formed with the digits 1, 2, 3, 4, 5 and 6 (repetition allowed). What is the value of x? | Difficult |
| A. 432 B. 1296 C. 648 D. None of these |